—127→
CECCS (Center for Research on Cognitive Science and Semiotics) COS/PUC-SP, Brasil14
En este artículo vamos a presentar los resultados parciales de un estudio que actualmente estamos desarrollando en el ámbito de la —128→ semiótica peirceana, más específicamente en el campo de las clasificaciones sígnicas de Charles S. Peirce. Creemos que la estrategia adoptada en este estudio, que llamamos Sign-Design, puede ser generalizada como un método de investigación en el campo de la semiótica. Se trata del abordaje sistemático de aspectos específicos de la teoría del signo de Peirce, que tiene como objetivo la construcción de modelos visuales de estructuras y procesos sígnicos, estableciendo conexiones entre la semiótica peirceana y los campos del diseño gráfico y del razonamiento diagramático (diagrammatic reasoning). Ella extrae del diseño gráfico una posible metodología y del campo de investigación, conocido como razonamiento diagramático, el argumento de que los diagramas son herramientas valiosas, no sólo para solucionar problemas específicos (problem solving), sino también, de una forma general, para la organización del pensamiento (cf. Chandrasekaran et al., 1995: xv-xxvii).
Lo que llamamos Sign-Design tiene una estrecha afinidad con propuestas desarrolladas por otros investigadores, que enfatizan sobre la relevancia de la creación de nuevos sistemas de notaciones y modelos gráficos en diferentes áreas (matemática, lógica, música, danza, etc.). Entre estas propuestas podemos citar lo que Shea Zellweger (1982: 17) llama «man-sing engineering» y lo que J.G. Long (1999) llama «notational engineering». Zellweger destaca la necesidad de exploración de un área aplicada y experimental de la semiótica, dedicada a la «creación de signos», basándose en «esfuerzos colectivos altamente especializados para comprender y mejorar nuestras herramientas mentales» (Zellweger 1982: 17-18). Según él, el principal desafío de este ámbito es proyectar signos capaces de establecer, a través de la «iconicidad visual» de sus «estructuras de superficie», un isomorfismo entre «la red de relaciones existentes en una sociedad de signos y la red correspondiente que existe en la estructura profunda de aquello que está siendo simbolizado» (Zellweger, 1982: 19-20). A este isomorfismo, Zellweger lo llama «iconicidad relacional». En la práctica, su plan se divide en dos partes: (i) identificación de las estructuras abstractas que serán simbolizadas; y (ii) invención de un sistema de signos que incorpore y revele, visualmente, las relaciones presentes en estas estructuras. En numerosos artículos, Zellweger ha demostrado los resultados de sus esfuerzos en el campo de la lógica elemental (Zellweger, 1982, 1991, 1992, 1997a, 1997b).
Lo que presentaremos, en las próximas secciones, es una posible metodología para Sign-Designy dos ejemplos de su aplicación. El —129→ resultado de este esfuerzo es un conjunto de herramientas visuales utilizadas para modelar tópicos complejos de la teoría del signo de Peirce.
Una posible metodología para Sign-Design propugna:
(i) Fase de conceptualización: en la que son estudiadas las bases teóricas y conceptuales para el diseño de estructuras y procesos sígnicos específicos. En los ejemplos que presentaremos, la fase de conceptualización incluye una detallada investigación del modelo del signo y su descripción en diferentes tipos, a través de las clasificaciones sígnicas.
Para Peirce, el signo es una relación lógica irreductiblemente triádica (CP 4.9)15. Cualquier descripción de procesos sígnicos implica un complejo constituido por tres términos indisolublemente relacionados -la tríada Signo-Objeto-Interpretante-. La Gramática Especulativa describe diferentes tipos de signos, a través de clases, en el contexto de diferentes clasificaciones sígnicas. Las clases son resultado de diferentes tipos de relaciones entre los términos de la tríada S-O-I, de acuerdo con las categorías cenopitagóricas (primeridad, segundidad y terceridad) y de acuerdo con las diferentes perspectivas en que la tríada S-O-I puede ser examinada (ver Houser, 1991: 432; Fredman, 1996: 150).
Las clasificaciones propuestas por Peirce tienen como base las relaciones entre las tricotomías. La más simple de las clasificaciones -Icono, índice y Símbolo- considera apenas una tricotomía (relación entre el Signo y su Objeto). La división en 10 clases de signos considera 3 tricotomías, la división en 28 clases considera 6 tricotomías y la división en 66 considera 10 tricotomías. La perspectiva descrita por cada tricotomía, así como las relaciones entre las tricotomías, se basan en 3 categorías -primeridad, segundidad y terceridad- y en el modo cómo, a través de la praecisio, están relacionadas (ver Savan, 1987-88: 14)16.
—130→(ii) Fase de desarrollo: en la que los resultados de la fase de conceptualización son aplicados al diseño de un nuevo modelo. Se trata de una fase eminentemente práctica, fundamentada en la traducción visual de los elementos teóricos examinados en la fase anterior. En las próximas secciones, a través de la presentación de ejemplos, discutiremos, sobre todo, esta fase.
(iii) Fase de experimentación: en la que son probadas las informaciones visuales proporcionadas por el modelo construido en la fase de desarrollo. Los resultados de esta fase son comparados y evaluados en vista de la fase de conceptualización. Resaltamos que estos modelos, más que ilustraciones de aspectos de una teoría, deben funcionar como herramientas visuales de investigación de esta teoría.
Peirce dejó, además de la más importante y conocida clasificación de signos, formada por tres clases (Icono, Indice, Símbolo), otras muchas clasificaciones sígnicas (divisiones en 10, 28 y 66 clases de signos). Peirce describió cuidadosamente la primera de estas clasificaciones (10 clases) para la cual creó dos diagramas (CP 2.264 8.376)17. No puede decirse lo mismo sobre las 28 y 66 clases. Éstas no recibieron un tratamiento tan completo como las 10 clases y existen divergencias entre los estudiosos de Peirce (Marty, 1990; Merrell, 1991; Houser, 1992: 502; Müller, 1993) respecto a los elementos fundamentales que forman estas clasificaciones: las tricotomías (diferentes perspectivas en que la tríada S-O-I puede ser examinada) y la orden de determinación («orden de aparición») de estas tricotomías.
Para entender mejor los problemas asociados a estas clasificaciones, desarrollamos un método para representar, visualmente, cualquier clasificación de signos a través de lo que llamamos diagramas triangulares. Este método surge a raíz del descubrimiento de ciertos principios lógico-diagramáticos en la construcción de los dos diagramas para las 10 clases de signos propuestos por Peirce en 1903 y 1908 (CP 8.376 y 2.264, figuras 1 y 2).
—131→
Figura 1: Diagrama con 10 clases de signos que fue dibujado por Peirce en una carta para Lady Welby, diciembre de 1908 (L463: 146, CP 8.376, EP2: 491).

Figura 2: Diagrama con 10 clases de signos dibujado por Peirce en su Syllabus de 1903 (MS 540: 17, CP 2.264, EP 2: 296).
Una vez identificados, estos principios permiten la construcción de diagramas para clasificaciones basadas en cualquier número de tricotomías. En otras palabras, observamos un patrón común en la composición de los diagramas de clases 3-tricotómicas (las 10 clases) y generalizamos el uso de este patrón para el diseño de diagramas de —132→ clasificaciones n-tricotómicas de signos (6-tricotómicas en el caso de las 28 clases; y 10-tricotómicas en el de 66 clases). Una vez que estos diagramas tienen como base el mismo principio, podemos utilizar lo que sabemos respecto a las 10 clases para comparar diferentes hipótesis sobre las 28 y 66 clases propuestas por los estudiosos del tema.
En una de las cartas que escribió a Lady Welby (L463: 146, CP 8.376, EP2: 491), Peirce dibujó el diagrama mostrado en la figura 1. Si comparamos esta figura con otro diagrama para las 10 clases encontrado en el Syllabus de 1903 (MS 540: 17, CP 2.264, EP2: 296; figura 2), podemos apreciar que muestra las mismas 10 clases en la misma posición relativa, aunque su estructura esté reflejada en un eje vertical18. Observamos un patrón común en la estructura de estos dos diagramas al traducirlos en coordenadas triangulares.
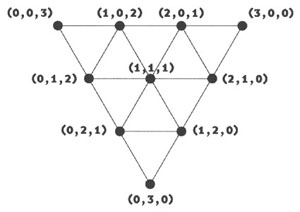
El primer paso es entender cada clase como una secuencia de cantidades de números «1», «2» y «3», que será transformada en un triplet (una secuencia de tres números), que equivale a una posición dentro de una red de coordenadas triangulares. Por ejemplo, la clase 111, que corresponde a tres «1»s, cero «2»s, y cero «3»s, es transformada en el triplet [3, 0, 0]; y la clase 321 es transformada en el triplet [1, 1, 1]. La suma de las cantidades de «1»s, «2»s y «3»s que forman cada triplet, en el contexto de las 10 clases, siempre será igual a 3. Esto se debe a que estamos trabajando con clases 3-tricotómicas, o sea, cada una de las 10 clases equivale a una secuencia de exactamente 3 números enteros, que varían de 1 a 3. Las posiciones de las clases son dispuestas entonces en coordenadas triangulares, según la figura 3.
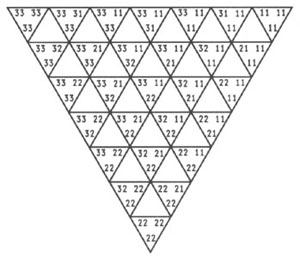
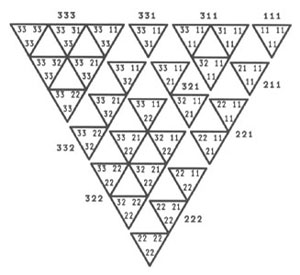
A partir de esta estructura con 10 vértices o posiciones, podemos transformar, nuevamente, los triplets en clases. Dibujando triángulos alrededor de estas posiciones, obtenemos un diagrama (figura 4) muy parecido19 al de la figura 1. Si invertimos las cantidades de «1»s y «3»s —133→ representadas en los triplets (de modo que el triplet [3, 0, 0] corresponda a la clase 333, etc.) y dibujamos cuadrados, en vez de triángulos, alrededor de los mismos vértices (figura 5), obtenemos exactamente la posición de las 10 clases encontradas en el segundo diagrama de Peirce (figuras 2 y 5).

Figura 4: El diagrama para Lady Welby (figura 1) dibujado a partir de las coordenadas triangulares para 10 clases.
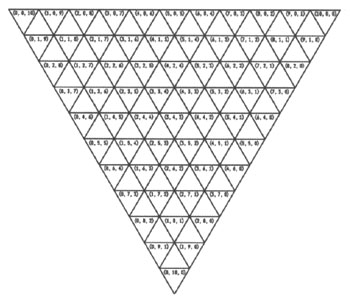
Este mismo método puede ser utilizado para la construcción de diagramas triangulares para las 28 y 66 clases de signos. Las 28 clases equivalen —134→ a secuencias de exactamente 6, y las 66 a secuencias de exactamente 10 números enteros, siempre variando de 1 a 3. Y ello porque las 28 clases son 6-tricotómicas y las 66 clases 10-tricotómicas. Estas secuencias pueden ser traducidas en triplets (conjuntos de tres números, cuya suma corresponde al valor tricotómico de la clasificación), que indican la posición relativa de una determinada clase en coordenadas triangulares. Los diagramas obtenidos se muestran en las figuras 6 y 7:

Figura 5: El diagrama del Syllabus (figura 2) dibujado a partir de las coordenadas triangulares para 10 clases.
Veremos algunos breves ejemplos de cómo estos diagramas pueden ser utilizados, traduciendo visualmente algunas hipótesis divergentes con relación a las 28 y 66 clases. Partiremos de la suposición de que es posible establecer correspondencias entre estas clasificaciones y la clasificación en 10 clases20. Las 10 clases servirán así como referencia para nuestras comparaciones21.
En relación a las 28 clases, una primera hipótesis parte de la observación de nuestro diagrama triangular (figura 6) y su similitud con el diagrama dibujado por Peirce en la carta escrita a Lady Welby (figura l). Ambos están formados por el mismo número de células (en este caso triángulos) aunque en el diagrama de Peirce no estén todas ocupadas.
—136→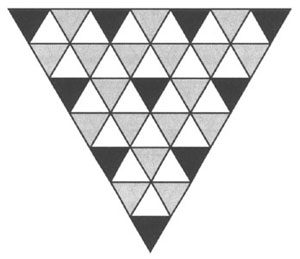
Figura 8: 10 clases de signos (en negro) en el contexto de las 28 clases (en negro o gris), según la hipótesis propuesta por los autores al respecto del diagrama para Lady Welby (figura 1).
Según esta hipótesis, si Peirce estuviese considerando las 28 clases mientras construía este diagrama, los diez triángulos ocupados corresponderían a clases especiales, aquéllas, dentro del contexto de las 28 clases, que equivalen a las 10 clases de signos (figura 8). En términos de tricotomías, esto significa que las clases 6-tricotómicas que siguen el patrón22 (h1 =h2=t1, h3=h4=t2, h5=h6=t3) son equivalentes a las 10 clases de signos. Peirce, sin embargo, no hace ninguna afirmación a este respecto.
Otra hipótesis (figura 9), propuesta por Ana Maróstica (1992: 117-120), indica, como correspondientes, otras clases. Ella considera que las tricotomías que se hallan en las 28 clases son [h1(S), h2(Oi), h3(Od), h4(Ii), h5(Id), h6(If)], mientras las que se hallan en las 10 clases son [t1(S),t2(0), t3(1)]. Para Maróstica, la correspondencia entre estas dos divisiones de signos sigue el patrón [h1=t1, h2=h3=t2, h4=h5=h6=t3].
—137→
Figura 9: 10 clases de signos (en negro) en el contexto de las 28 clases (en negro o gris), según la hipótesis formulada por Maróstica (1992: 117-120).
Una tercera hipótesis, propuesta por Robert Marty (1990: 209-228), sugiere que no es posible establecer correspondencias una a una entre las clases pertenecientes a las dos clasificaciones. Para Marty, cada una de las 10 clases corresponde, no a una clase, sino a un grupo específico de ellas, en el contexto de las 28 clases. Según Marty, las tricotomías de la división 6-tricotómica son [h1(Od), h2(Oi), h3(S), h4(If), h5(Id), h6(Ii)], y las clases formadas por estas tricotomías pueden ser consideradas subdivisiones de las 10 clases conforme al patrón [h1=t1, h3=t2, h4=t3]. Según podemos observar en la figura 10, para cada una de las 10 clases encontramos una o más clases correspondientes en el contexto de las 28.
En relación a las 66 clases, a través de una apreciación parecida a la de Marty, podemos comparar dos hipótesis sobre la orden de determinación de las tricotomías que componen esta clasificación (sugeridas por Weis & Burks, 1945 y Lieb, 1977; ver figuras 11 y 12). Podemos notar que el número de clases varía, en algunos casos de forma drástica (comparar, por ejemplo, las áreas correspondientes a las clases 111 y 331 en los dos diagramas), debido a la variación en el orden de determinación de las tricotomías. Para Weiss & Bruks, el orden de determinación de las tricotomías es [d1(S), d2(Oi), d3(Od), d4(S-Od), d5(Ii), d6(Id), d7(S-Id), d8(If), d9(S-If), d10 (S, Od, If)], mientras que para Lieb el orden es [d1 (Od), d2(Oi), —138→ d3(S), d4(Ii), d5(Id), d6(If), d7(S-Od), d8(S-Id), d9(S-If), d1O(S, Od, If)]23.
Son muchos los esfuerzos para modelar diagramáticamente las clasificaciones de signos de Charles S. Peirce (ver Marty, 1990; Merrell, 1991 y 1997; Balat, 1990; Liszka, 1996). Sin embargo, una investigación de los diagramas propuestos por Peirce y por sus estudiosos (cf. Farias & Queiroz, 1999) revela algunos límites impuestos por la naturaleza monocromática, bidimensional y estática de estos objetos. En SANDERS I, un proyecto para la construcción de un diagrama dinámico de las 10 clases de signos de Peirce, dirigimos nuestra atención a un aspecto particular de —139→ —140→ su teoría del signo: la posibilidad de representar diagramáticamente las relaciones sígnicas, en el dominio restringido a 10 clases de signos, sin descuidar las propiedades de interconexión entre las clases. El objetivo fue elaborar un diagrama donde sea posible observar tanto las relaciones entre tricotomías como las relaciones entre las clases.
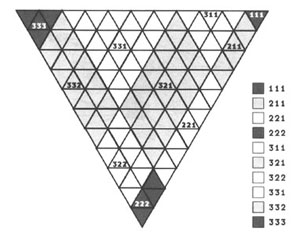
Figura 11: Correspondencias entre las 10 y las 66 clases de signos según el orden de determinación propuesto por Weis & Burks (1945).
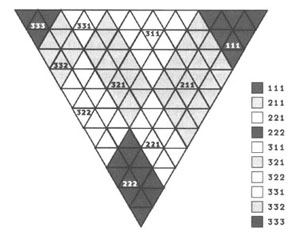
Figura 12: Correspondencias entre las 10 y las 66 clases de signos según el orden de determinación propuesto por Lieb (1977).

Figura 13: Diagrama propuesto por Balat (1989-91:86). Las clases están divididas en 3 subconjuntos que corresponden a las 3 tricotomías: (I, II, III) para la primera, (A, B, C) para la segunda y (1, 2, 3) para la tercera. Las conexiones orientadas corresponden a relaciones entre las 10 clases de signos.
La fase de desarrollo de SANDERS I tomó como punto de partida una estructura presentada por Michel Balat (1989-91: 86, figura 13). Siendo diferente a la mayoría de los diagramas para las 10 clases de signos de Peirce, éste, aunque bidimensional, sugiere una tercera dimensión espacial. Podemos observar en este diagrama que las tricotomías de Signo, Objeto e Interpretante están distribuidas en 3 ejes, de acuerdo con una notación según la cual I, A e 1 se refieren a la primeridad; II, B, 2 se refieren a la segundidad; III, C y 3 se refieren a la terceridad. Los números romanos (I, II, III) se distribuyen en el eje del Signo; las letras (A, B, C) en el eje del Objeto; y los números arábigos (1, 2, 3) en el eje del Interpretante La posición de cada una de las 10 clases se traduce en un conjunto de coordenadas que especifica su posición en el diagrama. Por ejemplo, la clase 111 corresponde a la coordenada (I, A, 1), localizada en el encuentro de los tres ejes del diagrama.
—141→En el diagrama que proponemos (figura 14), las clases conservan las mismas posiciones relativas, pero ahora están identificadas de acuerdo con otro formalismo visual. El primer paso fue considerar al Signo, al Objeto y al Interpretante como planos en intersección. En el espacio delimitado por estos planos, cada clase es representada como un cubo. Las tricotomías son representadas por la relación entre cada plano y las caras del cubo que le son paralelas. Las caras del cubo están pintadas de diferentes colores (gris oscuro, negro y gris claro), de acuerdo con las categorías (primeridad, segundidad, terceridad) que constituyen cada clase: gris oscuro para relaciones monádicas o de primeridad, negro para las relaciones diádicas o de segundidad, y gris claro para las relaciones triádicas o de terceridad. Por ejemplo, el cubo correspondiente a la clase 321 tiene sus caras paralelas al plano del Signo pintadas en gris claro, las caras paralelas al plano del Objeto pintadas de negro, y las paralelas al plano del Interpretante pintadas de gris oscuro. En conformidad con este formalismo, el cubo correspondiente a la clase 222 tiene todas sus caras pintadas de negro (ver figura 15).
Llegamos a la conclusión de que, si apenas 3 colores están disponibles, y si las caras paralelas de un cubo deben tener el mismo color, no existen más que diez maneras diferentes de pintarlo (ver figura 16). Esta conclusión puede ser entendida como una traducción visual de la fórmula matemática (n+1) (n+2) / 2 que define, según Weiss & Burks (1945: 387), la cantidad de clases de signos posibles a partir de un cierto número (n) de tricotomías.
—142→
Figura 16: Los únicos diez modos diferentes de pintar las caras paralelas de un cubo utilizando 3 colores.
El formalismo arriba presentado nos permite describir las relaciones entre tricotomías que forman las clases. En cuanto a las relaciones entre clases, éstas pueden ser divididas en dos grupos: relaciones estáticas, determinadas por la posibilidad de dividir las 10 clases en subgrupos (Iconos, Índices y Símbolos); y relaciones dinámicas, determinadas por la posibilidad de observar las 10 clases en interacción.
En relación a las relaciones estáticas, es importante destacar que SANDERS I, siendo un modelo informático, tridimensional e interactivo, permite que el observador navegue a su alrededor y fácilmente perciba relaciones significativas entre grupos especiales de clases/grupos. Es posible, por ejemplo, observar SANDERS I desde el punto de vista del plano del Objeto (ver figura 17) y, rápidamente, percibir la existencia de tres subgrupos de cubos o clases: los que tienen caras grises oscuras paralelas a este plano (Iconos), los que tienen caras negras paralelas a este plano (Índices), y los que tienen caras grises claras paralelas a este plano (Símbolos). Lo mismo ocurre cuando observamos el diagrama desde el punto de vista de los planos del Signo o del Interpretante.
Las relaciones dinámicas son representadas, en SANDERS I, por variaciones de tamaño y movimiento de los cubos. En el ejemplo que —143→ presentamos a continuación (ver el story board en la figura 18), mostramos cómo las relaciones, presentes en el diagrama de Balat (figura 13) —144→ en forma de flechas, están representadas en SANDERS I. Adoptamos dos reglas visuales diferentes para representar los dos tipos de relación que puede haber entre las clases24: (i) relaciones de instanciación, representadas por la sustitución de las clases instanciadoras por las clases instanciadas y (ii) relaciones de envolvimiento, representadas por la aparición simultánea de las clases relacionadas, donde las clases que envuelven son representadas por cubos mayores. Este formalismo puede ser entendido de la siguiente manera: cubos/clases mayores envuelven a los menores. De acuerdo con estas reglas, si en el estado 1 tenemos la clase 333, en el estado siguiente tendremos las clases 332 (por la relación de instanciación entre 333 y 332) y 331 (por la relación de envolvimiento entre 332 y 331).

Figura 17: Sanders I observado del punto de vista del plano del Objeto: Iconos (a la izquierda, en gris oscuro), Índices (en el centro, en negro) y Símbolos (a la derecha, en gris claro).

Figura 18: Un story board de las relaciones encontradas en el diagrama de Balat (figura 13), utilizando Sanders I.
Presentamos en este trabajo una estrategia de investigación en el campo de la semiótica peirceana que denominamos Sign-Design. Discutimos una posible metodología para esta estrategia y dos ejemplos, realizados por nosotros, de su aplicación. Estos dos ejemplos están aún realizándose y deben ser implantados en breve en forma de aplicativos informáticos.
Conforme hemos mencionado, estos modelos deben funcionar como herramientas visuales de investigación. Si el modelo está bien desarrollado, seremos capaces de pretender y probar visualmente ciertas hipótesis en relación a los procesos y estructuras sígnicas especificadas en la fase de conceptualización (fase i). En relación con todo el proceso, creemos que una mejor estrategia de diseño en la fase de desarrollo (fase ii), deberá llevar a un modelo más productivo en la fase de experimentación (fase iii). Complementariamente, flaquezas o inconsistencias en la fase de experimentación (fase iii) llevarán a una reconsideración de las premisas asumidas en la fase de conceptualización (fase i) y de las estrategias utilizadas en la fase de desarrollo (fase ii).
Lo que presentamos en este artículo corresponde específicamente a la fase de desarrollo. La fase de experimentación, propiamente dicha, —145→ conllevaría pruebas con los modelos informáticos que se implantarán según las especificaciones sugeridas por la fase de desarrollo. Sin embargo, el estado actual de este trabajo es ya capaz de revelar el potencial investigador de un abordaje diagramático de las clasificaciones sígnicas de Peirce.
BALAT, Michel (1989-1991). «Sémiotique et psychanalyse». Manuscrito.
———. (1990). «Type, Trace, Ton, le ‘ton’ peircien». Semiosis 57-58.
CHANDRASEKARAN, B.; GLASGOW, Janice; & NARAYANAN, N. Hari (eds.) (1995). Diagrammatic reasoning: cognitive and computational perspectives. Cambridge: MIT.
FARIAS, Priscila & QUEIROZ, João (1999). «Notes for a dynamic diagram of Charles Peirce’s classifications of signs». Semiótica (en prensa).
———. (2000). «On a diagrammatic method for the understanding of Peirce’s 10, 28, and 66 classes of signs». Proceedings of the 7th Congress of the International Association for Semiotic Studies (en prensa).
FREADMAN, Anne (1996). «Peirce’s second classification of signs». En Peirce’s doctrine of signs: theory, applications, and connections, V. M. Colapietro & Thomas M. Olshewsky (eds.), 143-159. Berlin: Mouton de Gruyter.
HOUSER, Nathan (1991).«A Peircean classification of models». En On semiotic modeling, M. Anderson & F. Merrell (eds.), 431-439. Berlin: Mouton de Gruyter.
———. (1992). «On Peirce’s theory of propositions: a response to Hilpinen». Transactions of the Charles Sanders Peirce Society23.3, 489-504.
JAPPY, A. (1984). «Peirce’s third trichotomy and two cases of sign path analysis». Semiotica 49, ½, 15-26.
———. (1989). «Peirce’s sixty-six signs revisited». En Semiotics and Pragmatics Proceedings of the Perpignan Symposium on Semiotics and Pragmatics 1983), G. Deledalle (ed.). 143-153. Amsterdam: John Benjamins.
KENT, Beverley (1987). Charles S. Peirce: logic and the classification of the sciences. Montreal: McGill-Queens University.
LIEB, Irwin C. (1977). «Appendix B». En Semiotics and significs: the correspondence between Charles S. Peirce and Victoria Lady Welby, C. S. Hardwick (ed.). Bloomington: Indiana University.
LISZKA, James (1996). A general introduction to the semiotic of Charles Sanders Peirce. Bloomington: Indiana University.
MARÓSTICA, Ana H. (1992). «Ars Combinatoria and time: Llull, Leibniz and Peirce». Studia Llulliana 32, 105-134.
—146→MARTY, Robert (1990). L’algebre des signes. Amsterdam: John Benjamins.
MERRELL, Floyd (1991). «Thought- signs, sign-events». Semiótica 87, ½, 158.
———. (1994). «Of signs and life». Semiótica 101, 3/4, 175-240.
———. (1997). Peirce, signs and meaning. Toronto: University of Toronto.
MÜLLER, Ralf (1993). On the principles of construction and the order of Peirce’s trichotomies of signs». Transactions of Charles S. Peirce Society XXX.1, 135-153.
PEIRCE, Charles S. (1994 [1866-1913]). The Collected Papers of Charles Sanders Peirce. Edición electrónica que reproduce los vols. I-VI [C. Hartshorne, & P. Weiss (eds.), Cambridge: Harvard University, 1931-1935], vols. VII-VIII [A. W. Burks (ed.), Cambridge: Harvard University, 1958]. Charlottesville: Intelex Corporation. [Citado aquí como CP, seguido del número del tomo y párrafo.]
———. (1976). New Elements of Mathematics by Charles S. Peirce, vol. 4, C. Eisele (ed.). The Hague: Mouton. [Citado aquí como NEM, seguido del número de página.] ___ (1998 [1893-1913]). The essential Peirce: selected philosophical writings, vol. 2, Peirce Edition Project (ed.). Bloomington: Indiana University. [Citado aquí como EP2, seguido del número de página.]
ROBIN, Richard S. (1967). Annotated catalogue of the papers of Charles S. Peirce. Amherst: University of Massachusetts. [Las referencias a los manuscritos y cartas de Charles S. Peirce -MS y L- proceden de este catálogo.]
SANDERS, Gary (1970). «Peirce sixty-six signs?». Transactions of Charles Sanders Peirce Society 6, 1, 3-16.
SAVAN, David (1987-88). An introduction to C. S. Peirce’s full system of semiotic (= Monograph Series of the Toronto Semiotic Circle, vol. 1). Toronto: Victoria College.
SERSON, Breno (1997). «On Peirce’s pure grammar as a general theory of cognition: from the thought-sign of 1868 to the semiotic theory of assertion». Semiótica113, ½, 107-157.
WEISS, Paul & BURKS, Arthur (1945). «Peirce’s sixty-six signs». Journal of Philosophy XLII, 383-388.
ZELLWEGER, Shea (1982). «Sign-creation and man-sign engeneering». Semiótica 38, ½, 17-54. ___ (1991). «Peirce, iconicity, and the geometry of logic». En On semiotic modeling, M. Anderson & F. Merrell (eds.), 483-507. Berlin: Mouton de Gruyter.
———. (1992). «Cards, mirrors, and hand-held models that lead into elementary logic». 16th Annual Conference of the International Group for the Psychology of Mathematics Education (offprint).
———. (1997a). «On a deep correspondence between sign-creation in logic and symmetry in cristallography». En Semiotics Around the World: Synthesis in Diversity (=Proceedings of the 5th Congress of the —147→ International Association for Semiotic Studies), I. Rauch & G. Carr (eds.) (offprint).
———. (1997b). «Untapped potential in Peirce’s iconic notation for the sixteen binary connectives». En Studies in the Logic of Charles Sanders Peirce, N. Houser, D. Roberts & J. Evra (eds.), 334-386. Bloomington: Indiana University.