Haciendo así mover el limbo en la tercera observación, el nivel que le está adherido se disloca con él y deja de ser horizontal; pero se le suelta y trae a esta posición en que se acaba de fijarle por medio de registros. Lo propio se hace después de cada observación par. (N. del A.)

Para apreciar el error que ocasionaría una pequeña falta de verticalidad, prolonguemos el plano del limbo hasta la esfera celeste; la cortará según un círculo máximo que llamaremos HZ´H, fig. 76. El punto Z´, el más elevado de este círculo, será el falso zenit indicado por el instrumento, y la línea OZ´, tirada a este punto por el centro del limbo, será la vertical aparente en derredor de la cual se miden sobre el limbo las distancias al zenit. Sea ahora OZ la vertical verdadera, de suerte que Z´OZ sea la inclinación del plano del limbo sobre la vertical, ángulo que llamaremos I. Supuesto esto, si se tira desde O un rayo visual OS a una estrella cualquiera S, la distancia al zenit verdadero será el ángulo ZOS que llamaremos Z. Mas la falsa distancia medida sobre el limbo será el ángulo Z´OS, y a ésta llamaremos Z´. Los tres lados ZZ´,ZS,Z´S formarán sobre la esfera celeste un triángulo esférico, rectángulo en Z´, y en el cual se tendrá

cos Z = cos Z´ cos I;

de aquí se sacaría a Z conociendo a Z´. Empero sería menester hacer el cálculo con una exactitud minuciosa a causa del factor cos I, que discrepa muy poco de la unidad, porque la inclinación I, que puede quedar después de las comprobaciones anteriores, es necesariamente muy pequeña. Ésta es la razón de por qué es más sencillo buscar aproximadamente la diferencia de los ángulos Z y Z´. Para esto, sustituyamos por cos I su valor 1-2 sen2 I/2 I, y tendremos

cos Z´-cos Z = 2 cos Z´ sen2 I/2 I.

Ahora, cos Z´-cos Z = 2 sen I/2 (Z + Z´) sen I/2 (Z-Z´): y sustituyendo este valor, se halla

sen 1/2 (Z-Z´) = cos Z´ sen2 I/2 I/sen I/2 (Z + Z´);

es el seno de la mitad de la diferencia buscada esta es siempre positiva, mientras Z´ no llega a un ángulo recto. Por consiguiente, y dentro de este límite, la distancia verdadera sobrepuja siempre a la distancia observada: así debe ser, toda vez que Z es una hipotenusa. No pudiendo nunca la inclinación I ser más que de algunos minutos, el factor sen2 I/2 I, que se halla en el numerador, será siempre un número pequeño, y el denominador sen 1/2 (Z + Z´) será comparativamente muy considerable, aun a 1º de distancia del zenit. Así, por bajo de este término, la diferencia de los arcos será sumamente pequeña; se podrá, pues, entonces sin temor de error alguno suponer Z = Z´ en el segundo miembro, lo que equivale a despreciar el cuadrado de Z-Z´, y se hallará de este modo definitivamente,

sen I/2 (Z-Z,) = sen2 1/2 I/tang Z´;

Para apreciar la exactitud de esta fórmula, es preciso comparar los resultados que da con los sacados de la fórmula rigorosa cos Z = cos Z´ cos I. Suponiendo I = 10´ y Z = 1º sexag., se halla ya que las dos fórmulas concuerdan casi exactamente. Mas cerca del zenit, la aproximación disminuye, y por último deja de ser suficientemente exacta; por ejemplo, cuando Z´ es nula, da a Z´-Z infinita, en vez de que la fórmula rigorosa da entonces a cos Z = cos I, o Z = I, es decir, que todo el error de la vertical se transporta sobre la distancia al zenit, como así debe suceder con efecto.

De aquí deben sacarse dos conclusiones: la primera es que hay precisión de atenuar cuanto se pueda la falta de verticalidad; la segunda, que es menester evitar el observar muy cerca del zenit, donde es más sensible la influencia de esta falta sobre las distancias a causa del denominador tang Z´. Este último inconveniente es siempre nulo para la Polar, que sirve comúnmente para determinar las latitudes. Su distancia al zenit sale de los límites en que son considerables los errores de la verticalidad, por lo menos en todos los países habitables en que puede haber ocasión de observarla. Por último, cuando se observe cerca del zenit, aun a algunos grados de distancia, se hará bien en calcular, tan exactamente como se pueda, la inclinación del plano del limbo, y se la tendrá en cuenta por medio de la fórmula anterior, lo que atenuará siempre el error, y aun podrá hacer su influencia enteramente insensible. (N. del A.)

Estimemos el error que pudiera resultar de una falta de paralelismo del eje óptico. Para esto concibamos un rayo visual tirado al objeto observado, y que pase por el eje óptico del anteojo. El ángulo de este radio con la vertical será la distancia verdadera al zenit o Z; pero la distancia aparente Z´, tal como se la leerá sobre el limbo, no será más que la proyección de la anterior sobre el plano del mismo por medio de un arco de círculo perpendicular a su plano. Este arco medirá pues la inclinación del eje óptico sobre el plano del limbo. Sea I esta inclinación; es visible que los ángulos Z y Z´ e I son los tres lados de un triángulo esférico rectángulo, cuya hipotenusa es Z, y en el cual se tendrá por consiguiente

cos Z = cos Z´ cos I.

Esta ecuación es absolutamente de la misma forma que la que hemos hallado para la verticalidad del limbo. Sacaráse pues ella también por una aproximación suficiente siempre

sen I/2 (Z-Z´) = sen2 I/2 I/tan Z´.

El error procedente del eje óptico es todavía más pequeño que aquel que se debe a la verticalidad del limbo, a lo menos ordinariamente, porque es muy fácil evitar sobre la inclinación de dicho eje 1 minuto de error, y su efecto sería insensible sobre las distancias al zenit en que se acostumbra observar con el círculo repetidor. Se ve que este efecto tiende también a disminuir las distancias al zenit, toda vez que la distancia Z´ leída sobre el limbo es menor que la distancia real Z.

Si se hubiese arreglado mal el eje óptico, o si se hubiera observado demasiado lejos de este eje, se podrían siempre corregir las observaciones por medio de la fórmula anterior. (N. del A.)

Sea @ la distancia polar del astro que se observa, P su ángulo horario, Z su distancia zenital, D la distancia del zenit al polo o complemento de la latitud del lugar. Supuesto esto, en el triángulo esférico formado por los tres arcos @, Z y D, se tendrá al ángulo horario P por la fórmula

cos P = cosZ-cos @ cos D/sen @ sen D

Supongamos que al cabo de algunos minutos la distancia zenital se convierta en Z´, y en P´ el ángulo horario, conservándose las mismas @ y D, se tendrá así mismo

cos P´ = cos Z´-cos @ cos D/sen @ sen D;

restando estas dos ecuaciones una de otra, resultará

cos P´-cos P = cos Z-cos Z/sen @ sen D,

o trasformando estas expresiones

sen I/2 (P´ + P) sen I/2 (P´-P) = sen I/2 (Z´ + Z) sen I/2 (Z´-Z)/sen @ sen D.

Si las observaciones son bastante próximas para que las diferencias P´-P y Z´-Z puedan considerarse como muy pequeñas, podrá sustituirse la relación de los arcos a la de los senos, y se tendrá

P´-P = (Z´-Z) sen I/2 (Z´ + Z)/sen I/2 (P´ + P) sen @ sen D;

además si se desprecian los cuadrados y las potencias superiores de estas pequeñas cantidades, se podrá en el factor sen I/2 (Z´ + Z)/sen I/2 (P´ + P) que multiplica ya a Z´-Z en el segundo miembro, suponer Z = Z´ y P = P´, lo cual dará

P´-P = (Z´-Z) sen Z/sen P sen @ sen D.

Las circunstancias mas favorables a la determinación del ángulo horario son las que dan a P´-P los valores más pequeños, manteniéndose la misma Z´-Z; porque entonces un pequeño error sobre Z influirá poco sobre P. Es menester pues para la exactitud del coeficiente sen Z/sen P sen @ sen D sea el menor posible; y como relativamente a una misma estrella y a un mismo observador @ y D son constantes, la condición versa sólo sobre el factor sen Z/sen P. Ahora bien, si en el triángulo esférico formado por los tres arcos Z, @, y D se llama A al azimut opuesto al lado @, se tendrá sen Z/sen P = sen @/sen A; y como @ es constante, se ve que la condición impuesta quedará cumplida cuando sen A sea el mayor posible para el astro que se observa; por consiguiente, si éste puede en virtud de su posición pasar por el primer vertical, el máximum tendrá lugar cuando llegue a él, porque entonces el azimut A será igual a un ángulo recto.

Vese también que es preciso, para la misma estrella, evitar los ángulos horarios demasiado pequeños que hagan al denominador sen P o sen A una fracción muy reducida, y por consiguiente aumenten el valor de la relación sen Z/sen P o sen @/sen A. Tocante a la elección que haya de hacerse entre las diferentes estrellas, como todas no pueden pasar por el primer vertical, se ve que es preciso evitar aquellas cuya distancia polar @ es demasiado pequeña, y adherirse a las otras para las que es el mayor posible el seno de esta distancia, lo que se verifica respecto de las estrellas situadas en el plano del ecuador en que @ es igual a un ángulo recto, (N. del A.)

Todo esto se ve fácilmente por la fórmula

Z´-Z = (P´-P) sen P sen @ sen D/sen Z

que hemos hallado en la nota anterior. Esta fórmula supone que se parte de un primer valor de P y Z para pasar a otros extremadamente próximos P´ y Z´ y da a conocer el cambio Z´-Z de la distancia al zenit, cuando se conoce la variación P´-P del ángulo horario, la cual puede inferirse del tiempo transcurrido entre las dos observaciones. Mientras las diferencias Z´-Z y P´-P puedan suponerse muy pequeñas, estas diferencias serán sensiblemente proporcionales entre sí, y el término medio aritmético de las distancias zenitales corresponderá al de los ángulos horarios o de las épocas de las observaciones. Mas concíbese por esto mismo que tal hipótesis está limitada y no puede admitirse sino por un tiempo muy breve.

¿Quiere juzgarse en cada caso de su exactitud y de la extensión que puede dársele sin temor de error sensible? No hay más que partir de un valor dado de Z y de P, por ejemplo, de la distancia media observada durante una serie, y del ángulo horario medio que puede inferirse de ella por medio del triángulo esférico, con la fórmula vigorosa

cos P = cos Z-cos @ cos D/sen @ sen D.

Luego se supondrá en el ángulo horario un cambio igual a la mitad del intervalo de una serie, por ejemplo, de 5´ de tiempo sexagesimal, si las series son de 10 minutos, lo que, reducido a arco, forma un cambio de 1º15´ sexagesimales en P; entonces, con el nuevo valor P´ = P + 1º15´, se calculará la nueva distancia Z´ por la fórmula rigorosa

cos P = cos Z-cos @ cos D/sen @ sen D;

tendráse pues así a Z´, y por consiguiente a Z´-Z; se podrá pues comparar este valor con el que resulta de la fórmula aproximada

Z´-Z = (P´-P) sen P sen @ sen D/sen Z

Si concuerdan poco más o menos de modo que sólo resulte para Z´-Z una diferencia insensible, por ejemplo, 1/100 de segundo, se podrá sin escrúpulo emplear la fórmula aproximada en todo el intervalo de una serie, y por lo tanto, mirar a la distancia media sobre el limbo, como correspondiente a la época media de las observaciones. Pero si los dos valores de Z´-Z se apartan demasiado uno de otro para que pueda despreciarse su diferencia, se inferirá que se han prolongado sobradamente las series, y en consecuencia que será menester estrechar sus límites. En este cálculo es preciso partir de la época media como la más favorable; porque estando menos apartado de las extremas, prolonga menos la proporcionalidad de los ángulos horarios y de las alturas. (N. del A.)

Sea @ la distancia polar aparente de una estrella, es decir, la distancia polar afectada de la precesión, aberración y nutación; D la distancia del polo al zenit, o el complemento de la latitud del lugar en que se observa; por último llamemos Z a la distancia zenital observada corregida de la refracción, y P al ángulo horario pedido. Con estos datos se tendrá al ángulo P por la fórmula

sen I/2 P = 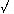símbolo sen (Z + @-D)/2 sen (Z + D-@)2/sen @ sen D

He aquí un ejemplo de este cálculo aplicado a una observación de Rigel, hecha en Dunkerque el 21 de marzo de 1809 a la latitud de 51º2´5´´ siendo la altura del barómetro 0m,76865, y estando a +6º el termómetro centesimal.

La distancia de Rigel al polo boreal del ecuador, tomada en el Conocimiento de los Tiempos, y reducida a posición aparente para el 21 de marzo de 1809, es@ = 98º26´8´´,35

La ascensión recta reducida a tiempo para el mismo día A = 5h5m22s,61

La observación hecha en el círculo repetidor después del paso de Rigel por el meridiano ha dado la distancia aparente al zenit 70º45´59´´,21

Corrección del nivel -0,47

70º45´58´´,74

Refracción calculada por las Tablas para la presión barométrica y la temperatura observadas 2´50´´,01

Distancia verdadera de Rigel al zenit en el instante medio de la observación Z = 70º48´48´´,75

Con estos datos se hace el cálculo como sigue:

@ = 98º26´8´´,35
D = 39º57´55´´,00
@-D = 59º28´13´´,35		59º28´13´´,35
Z = 70º48´48´´,75		70º48´48´´,75
Z + @-D = 130º17´2´´,10		Z + D-@ = 11º20´35´´,40
Z + @-D/2 = 65º8´31´´,05		Z + D-@/2 = 5º40´17´´,70
	log sen (Z + @-D/2) = 1,9577758	log sen @ = 1,9952758
	log (Z + D-@) = 2,9948723	log sen D = 1,7985466
	2,9526481	1,7938224
	1,7938224
	log sen2 I/2 P = 1,1588257
	log sen I/2 P = 1,5794128
	I/2 P = 22º18,48´´,8
	P = 44º37´37´´,6	= 2h58m30g,51

Ascensión recta aparente de Rigel, calculada y reducida a tiempo A = 5h 5m 22s,61

Suma o tiempo sideral de la observación 8h3m53s,12

Época media de la serie en tiempo del péndulo 5h46m30s,28

Retraso del péndulo sobre el tiempo sideral en la época de la observación de Rigel 2h17m22g,84

El cálculo precedente supone que se ha sabido calcular la distancia polar y la ascensión recta aparentes de Rigel para el día de la observación. Para ello es preciso conocer la precesión, la aberración y la nutación de la estrella para este mismo día, a fin de añadir estas cantidades a su posición media. En el tomo III se verá el modo de determinarlas.

Tocante a la refracción, se la tomará en las Tablas, porque tenemos explicado cómo éstas se hallan formadas. Se hallará una en el Conocimiento de los Tiempos.

La observación que acabamos de calcular había sido hecha después del paso de Rigel por el meridiano; y como Rigel es una estrella austral que no es visible más que en su paso por el meridiano superior, se ve que el ángulo horario P se ha encontrado contado naturalmente desde el meridiano superior en el sentido del movimiento diurno según los convenios hechos en el § 17. Ésta es la razón porque le hemos añadido la ascensión recta A para tener el tiempo sideral. Pero si a Rigel se le hubiera observado antes de su paso por el meridiano, habría sido preciso tomar el complemento de P, a fin de que este ángulo se contase siempre en el sentido del movimiento diurno, después de lo cual se le habría añadido el ángulo A, como hemos dicho arriba. En el tomo siguiente se hallará el cálculo de la hora por alturas absolutas del Sol. (N. del A.)

Se ha visto en la nota del § 280 que las distancias sucesivas de un astro al zenit, y los ángulos horarios que les corresponden, están ligados entre sí por la siguiente relación.

sen I/2 (Z´ + Z) seni I/2 (Z´-Z) = sen @ sen D sen I/2 (P´ + P) sen I/2 (P´-P).

Supongamos que Z representa la distancia meridiana, y Z´ otra observada muy cerca del meridiano; de modo que Z´-Z sea una cantidad muy pequeña que llamaremos d, la cual será positiva en los pasos superiores en que Z´ sobrepuja a Z, y negativa en los inferiores en que Z sobrepuja a Z´. Supongamos también que se cuentan los ángulos horarios a empezar desde el meridiano en que se observa el paso; el ángulo horario P, correspondiente a la distancia Z, será nulo, y el ángulo horario P´, correspondiente a Z´, muy pequeño. Verificando estas sustituciones en la relación anterior para hacerla aplicable a las distancias meridianas, se convertirá en

sen (Z + I/2 d) sen I/2 d = sen @ sen D sen2 I/2 P´

o desarrollando el primer factor

sen Z sen d + 2 cos Z sen2 I/2 d = 2 sen @ sen D sen2 P´

El valor exacto de sen d puede expresarse en una serie convergente, ordenada según las potencias de sen2 I/2 P´; pero se puede obtener sin cálculo alguno el primer término de este desarrollo que casi siempre basta. Porque, echando de ver que sen d y sen I/2 d son fracciones muy pequeñas, se advierte que el cuadrado de la última, o sen2 I/2 d será mucho menor que la primera; así que, despreciando este cuadrado en la primera aproximación se tendrá simplemente

sen d = 2 sen @ sen D sen2 I/2 P´/sen Z.

Puédese todavía simplificar esta expresión, o a lo menos hacer más cómodo su cálculo, notando que, en razón a ser d un arco muy pequeño, no hay inconveniente en suponer sin error sensible la proporción sen 1´´ : sen d : : 1´´ : d, es decir, que puede sustituirse a sen d la expresión d/1´´ sen 1´´, en cuyo caso se tendrá

d = sen @ sen D/sen Z; 2´´ sen2 I/2 P´/sen 1´´

Es el valor de la corrección pedida, la cual se encuentra así expresada en segundos. Como se tiene en general Z´-Z = d, resultará la distancia meridiana Z = Z´-d. Para establecer la continuidad entre las expresiones algebraicas, es preciso contar la distancia polar @, yendo del meridiano superior al inferior, y desde 0 hasta toda la circunferencia. Entonces @ será en todos los pasos superiores menor que dos ángulos rectos, sen @ será positivo, la corrección d se conservará positiva por el solo juego de la fórmula, y en su consecuencia se restará de las distancias al zenit observadas. Por el contrario, en los pasos del meridiano inferior, siendo @ mayor que dos ángulos rectos, sen @ se hará negativo, d cambiará de signo y se añadirá a las distancias zenitales.

Para aplicar la fórmula anterior se calculan los valores del factor 2´´ sen2 I/2 P´/sen 1´´, correspondiente a la época de las observaciones, se hace su suma y se la divide por el número de éstas. Luego se multiplica este resultado por el factor sen @ sen D/sen Z, que es constante para todas las series del mismo astro, y se tiene la corrección media que es preciso aplicar a la distancia observada en el sentido conveniente, según más arriba dijimos. (N. del A.)

La reducción al meridiano tiene por expresiva

d = sen @ sen D/sen Z; 2´´ sen2 I/2 P´/sen 1´´.

Supongamos que durante una revolución diurna del astro, el reloj señale 24h-r siendo r un corto número de oscilaciones. Sea T´ uno de los ángulos horarios observados en tiempo del reloj, es decir, el número de oscilaciones transcurridas entre la época de la observación, y el paso del astro por el meridiano: es visible que este ángulo horario convertido en arco, no tendrá por valor a 15 T´, como debería ser, si el reloj y el astro estuvieran acordes. Antes de hacer esta conversión, el número T´ deberá modificarse en la relación de la marcha del reloj con la del astro, es decir, en la relación de 24h-r a 24h, y multiplicando el resultado por 15 el valor del ángulo horario expresado en arco vendrá a ser 15T´24h/24h-r y, reduciendo todo a segundos sexagesimales, 15 T´ + 15 T´ r/86400-r. Tal será pues el valor de P´ que sería preciso emplear en el cálculo de la corrección de manera que haciendo para mayor sencillez 15 T´ = p´, y r/86400-r = r´, se tendría

P´ = p´-+p´r´.

Pero sustituyendo este valor en la expresión de d, puede aprovecharse la circunstancia de que r´ es una cantidad muy pequeña para simplificarla mucho. En efecto, se tiene

sen I/2 P´ = sen (I/2 p´ + I/2 p´r´) = sen I/2 p´ cos I/2 p´r´ + cos I/2 p´ sen I/2 p´r´.

Elevemos esta expresión al cuadrado; circunscribámonos a la primera potencia de sen I/2 p´r´, y despreciando a las otras como fracciones que son muy pequeñas, tendremos

sen2 I/2 P´ = sen2 I/2 p´ + sen p´ sen p´r´/2

Siendo sumamente pequeño el segundo término de este valor a causa de la pequeñez de los arcos p´ y p´r´ se puede sin error sensible sustituirle 2r´ sen2 I/2 p´; lo cual equivale a poner 2 sen2 I/2 p´ en vez de sen p´, y 2 r´ sen I/2 p´, en vez de sen p´r´. Obtiénese entonces esta expresión muy sencilla

sen2 = I/2 P´ = (1 + 2 r´) sen2 I/2 p´,

lo que da

d = sen @ sen D (1 + 2 r´)/sen Z. 2´´ sen2 I/2 p´/sen 1´´.

Por este artificio, cada corrección, calculada en virtud del ángulo horario verdadero, se halla en relación constante con la que se tendría empleando en el cálculo el ángulo horario dado inmediatamente por el reloj. Resulta sólo de aquí un término más en el factor constante, común a todas las reducciones. Así, cuando el reloj siga aproximadamente la marcha del astro observado, se efectuarán todos los cálculos como si la siguiese con exactitud; se determinarán los valores del factor 2´´ sen2 1/2 p´/sen 1´´, como de ordinario, y se cuidará en seguida de tomar en cuenta al factor 1 + 2 r´ en el cálculo del factor constante. O si se quiere, cuando se haya encontrado la corrección media de toda la serie, tal como sería si el péndulo siguiese la marcha del astro, se le añadirá el producto de esta corrección por el número abstracto 2r´. Es claro que r sería negativo, si el reloj adelantase respecto del astro en vez de atrasar, como aquí se ha supuesto. Esta aproximación sería también muy suficiente, aun cuando se observase al Sol con un reloj arreglado por el tiempo sideral o recíprocamente. (N. del A.)

Échase esto de ver inmediatamente por la expresión de d que contiene en su numerador al seno de la distancia polar. Tocante a la extensión de los ángulos horarios, conviene detener la serie cuando el error de 1´´ de tiempo diese en P´ uno de un segundo de grado en la reducción d. (N. del A.)

100

Sea Z´ la distancia media al zenit de las observadas en los pasos superiores; Z´ esta misma distancia media para los pasos inferiores; D la verdadera distancia del polo al zenit, y @ la distancia polar verdadera: calculando con estos valores, que suponemos exactos, se hallaría:

En los pasos superiores

D = Z´ + @,

En los inferiores

D = Z´´-@,

y estos dos valores de D concordarían entre sí. Mas, si en vez de @, se emplea @ + e, siendo e el error de la distancia polar, se hallarán necesariamente valores de D que no concordarán, y llamándolos D´ y D´´, se tendrá

En los pasos superiores D´ = Z´ + @ + e

En los inferiores D = Z´´ + @-e

o poniendo por Z´ + @ y Z´´-@ su valor común D,

D´ = D + e, D´´ = D + e

de donde se saca por adicción y sustracción

D = D´ + D´´/2 e = D´-D´´/2,

Así cuando se haya operado con una distancia polar inexacta, la semisuma de las distancias zenitales obtenidas por la observación de los dos pasos da la verdadera distancia del polo al zenit, y su semidiferencia hace conocer el error de la distancia polar. El error e influye a la verdad sobre el coeficiente constante que entra en la expresión de la reducción al meridiano; pero esta influencia se atenúa considerablemente por la fracción sen2 I/2 p´, como hemos notado. Por lo demás, si se temiera que fuese sensible, no habría más que calcular de nuevo las reducciones al meridiano con las distancias D, corregidas por la comparación de los pasos superiores e inferiores; lo que daría un nuevo valor de D, más exacto todavía que el primero. Pero en el estado actual de los catálogos astronómicos, nunca será preciso recurrirá esta segunda aproximación. (N. del A.)